Elementos de una elipse La elipse y algunas de sus propiedades geométricas. La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí: El semieje mayor (el segmento C-a de la figura), y; El semieje menor (el segmento C-b de la figura). Miden la mitad del eje mayor y menor respectivamente.. Ecuación de la elipse. Para definir la ecuación de la elipse, tenemos en cuenta su definición: d ( K, F) + d ( K, F ′) = 2 a. Desarrollando esto, llegamos a una relación entre las coordenadas del punto K ( x, y), que se verifican para todos los puntos de la elipse: x 2 a 2 + y 2 b 2 = 1. La ecuación general de la elipse cuyo centro está.

Concepto, elementos y tipos de elipse YouTube

Elementos y gráfica de la elipse YouTube
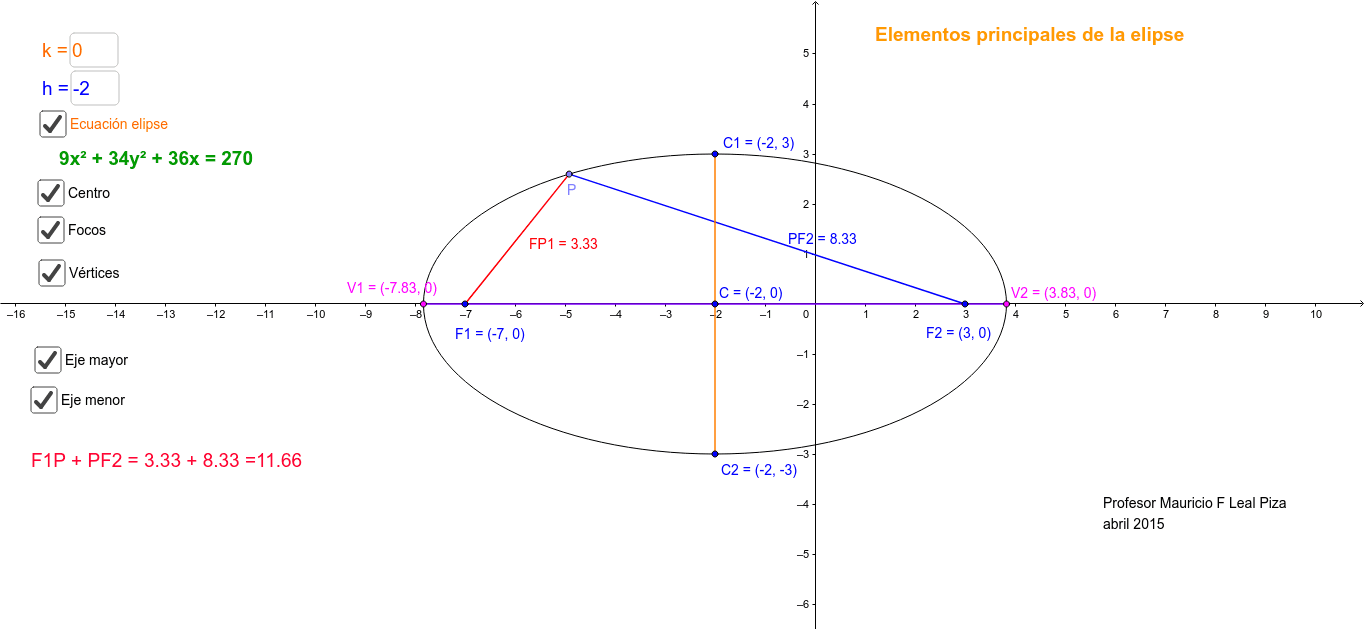
Cuales Son Los Elementos Del Elipse ajore

ELEMENTOS DE LA ELIPSE YouTube
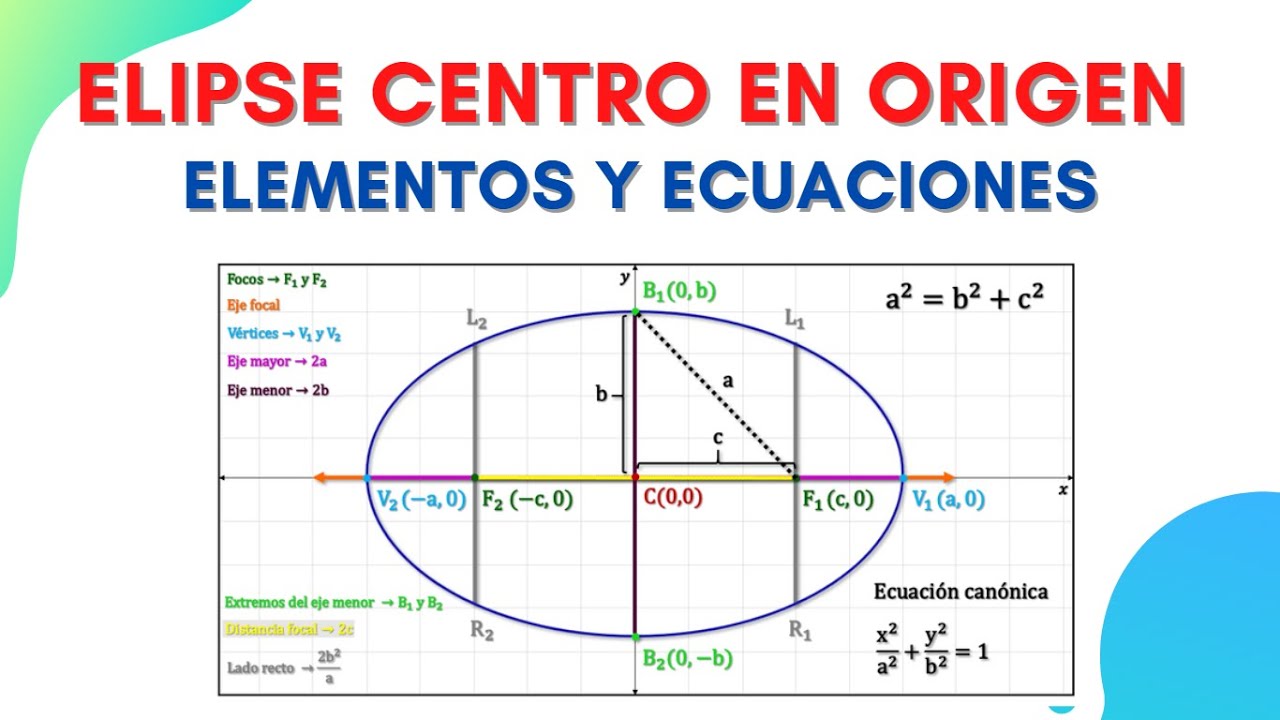
ELIPSE Centro en origen ELEMENTOS Y ECUACIONES Todo lo que debes saber, en menos de 7

ELIPSE. Cálculo de elementos. Ecuación. YouTube

Elipse elementos, tipos, ejemplos, ejercicios resueltos
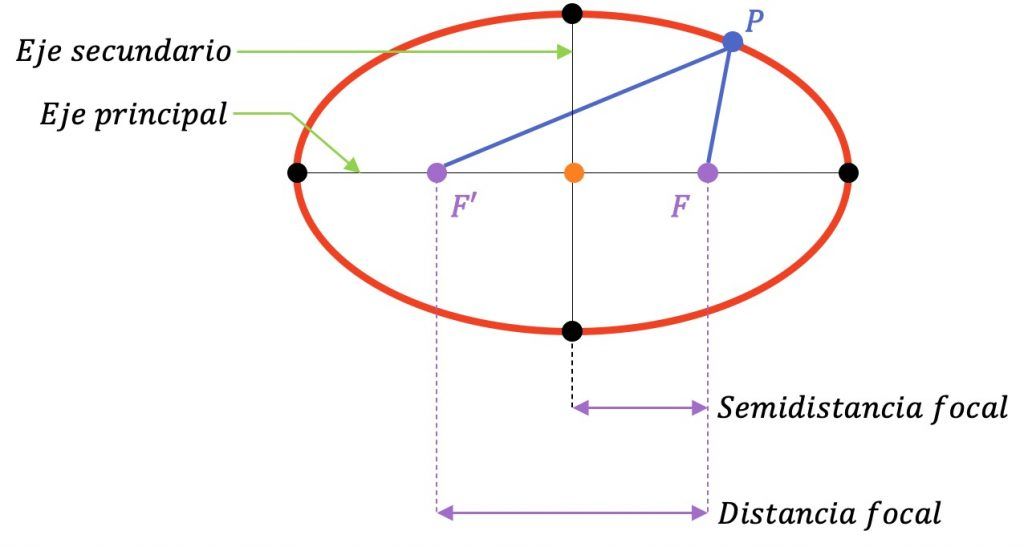
Cómo hallar la ecuación de la Elipse (fórmula y ejemplos)

Elementos de la elipse YouTube
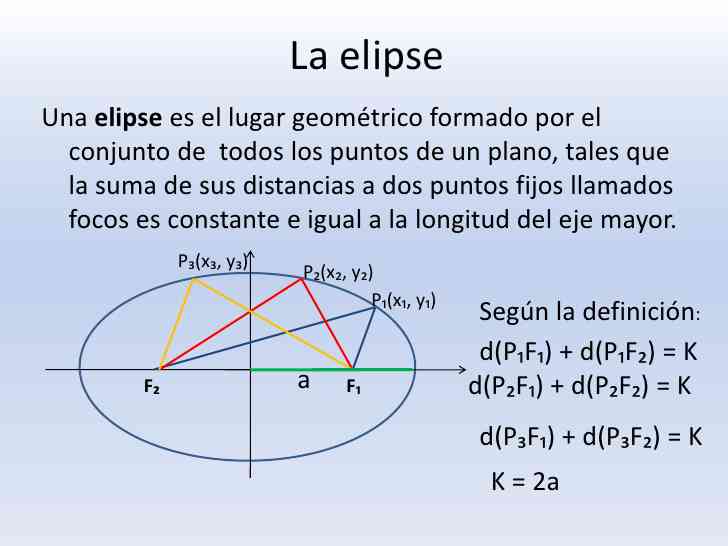
Partes de la elipse
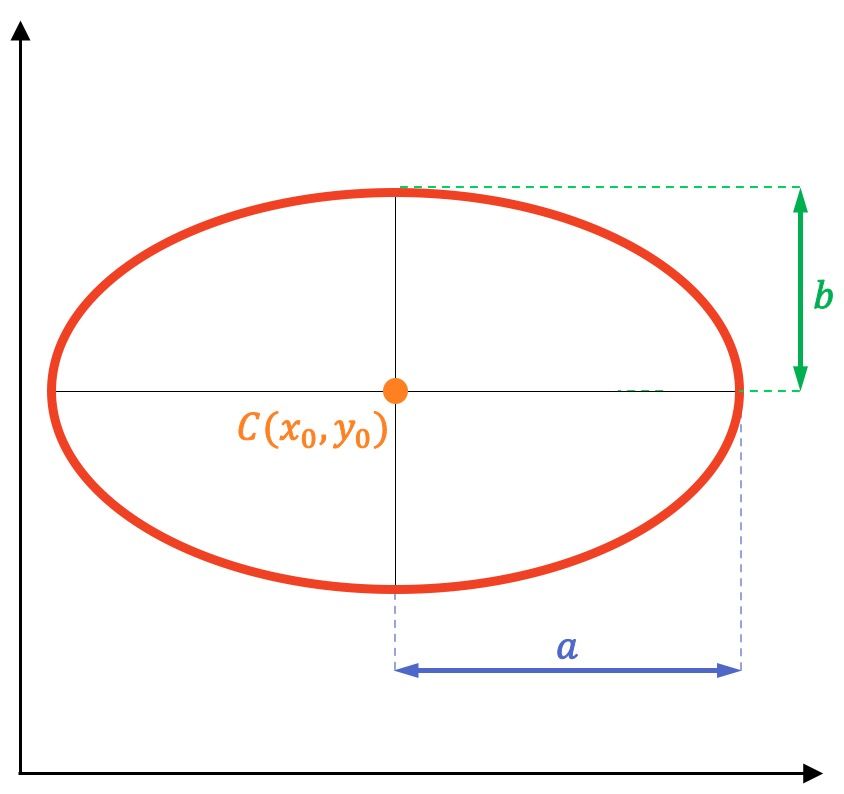
Cómo hallar la ecuación de la Elipse (fórmula y ejemplos)

TRAZADO DE UNA ELIPSE Y SUS ELEMENTOS PRINCIPALES YouTube

Definición, ecuación, fórmulas y elementos de la elipse YouTube

🏉 ELIPSE Concepto y elementos (focos, vértices, Eje Mayor, Eje Menor, L.R.) Juliana la profe

Calaméo Concepto y elemento de la elipse
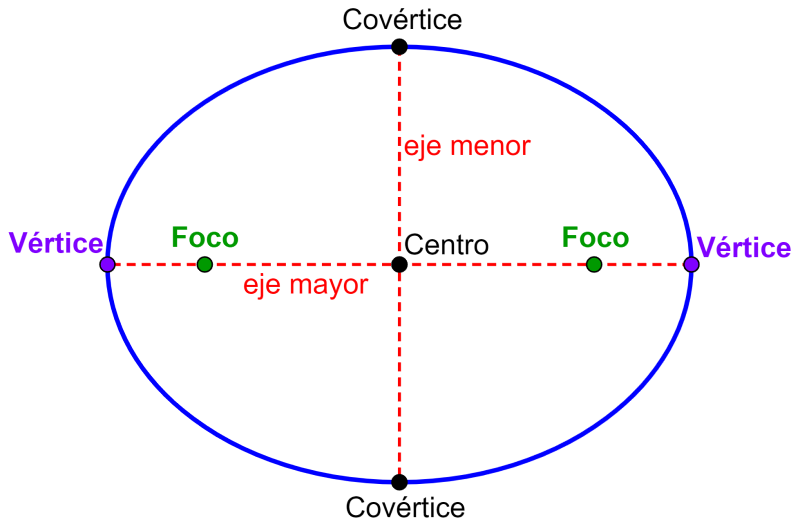
Elementos y Partes de la Elipse con Diagramas Neurochispas

ELEMENTOS DE UNA ELIPSE Mundo Genial de la Matemática

*Concepto y elementos de la elipse HD YouTube

Gráfica y elementos de la Elipse conociendo su ecuación general Ejemplo 1 YouTube
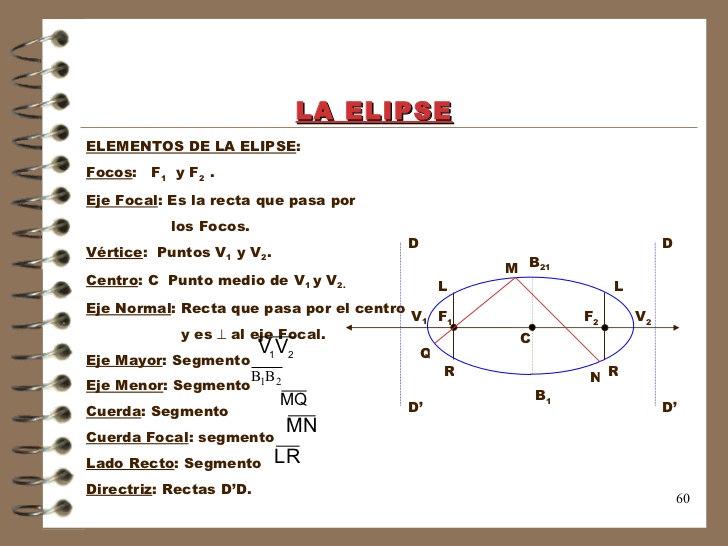
Matematicas 271 PARTES DE LA ELIPSE Y ECUACIÓN CON CENTRO EN EL ORIGEN
El área comprendida dentro de una elipse es π veces el producto de los dos semiejes (a y b). Ejemplo 2: Sea una elipse de semiejes conocidos, donde a = 6 cm y el menor b = 4 cm, calcule su área. Del enunciado del problema sabemos que a = 6 cm y b = 4 cm. Como A= π∙a∙b, entonces su área es: Por lo tanto, el área de la elipse es igual a.. Los ejes son del doble del radio correspondiente. El centro de la elipse está en el punto medio de los é vértices , que también es el punto medio de los é covértices . Los focos de la elipse se encuentran en el radio mayor . Su característica especial es que la suma de las distancias desde los focos a cada punto de la elipse es siempre.